- Created by Nicolas Stifani, last updated on Dec 19, 2024 33 minute read
You are viewing an old version of this page. View the current version.
Compare with Current View Page History
« Previous Version 66 Next »

This page provides a practical guide for microscope quality control. By following the outlined steps, utilizing the provided template files, and running the included scripts, you will have everything needed to easily generate comprehensive report on your microscope's performance.
Equipment used
- Thorlabs Power Meter (PM400) and sensor (S170C)
- Thorlabs Fluorescent Slides (FSK5)
- TetraSpeck™ Fluorescent Microspheres Size Kit (mounted on slide) ThermoFisher (T14792)
Software used
- FIJI FIJI
- MetroloJ_QC Plugin for FIJI MetroloJ_QC
- iText Plugin for FIJI iText
- R R from the CRAN R Project
- I typically use the integrated development environment (IDE) for R RStudio
Please note that during quality control, you may, and likely will, encounter defects or unexpected behavior. This practical guide is not intended to assist with investigating or resolving these issues. With that said, we wish you the best of luck and are committed to providing support. Feel free to reach out to us at microscopie@cib.umontreal.ca
Illumination Warmup Kinetic
When starting light sources, they require time to reach a stable and steady state. This duration is referred to as the warm-up period. To ensure accurate performance, it is essential to record the warm-up kinetics at least once a year to precisely define this period. For a detailed exploration of illumination stability, refer to the Illumination Power, Stability, and Linearity Protocol by the QuaRep Working Group 01.
Acquisition protocol
Place a power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
Center the sensor with the objective to ensure proper alignment.
Zero the sensor to ensure accurate readings.
Using your power meter controller (e.g., Thorlabs PM400) or compatible software, select the wavelength of the light source you want to monitor.
Turn on the light source and immediately record the power output over time until it stabilizes.
I personally record every 10 seconds for 24 hours and stops when it has been stable for 1 h.
- Repeat steps 3 to 5 for each light source you want to monitor
Keep the light source turned on at all times. Depending on your hardware, the light source may remain continuously on or be automatically shut down by the software when not in use.
Results
Use the provided spreadsheet template, Illumination_Warmup Kinetic_Template.xlsx, and fill in the orange cells to visualize your results. For each light source, plot the measured power output (in mW) against time to analyze the data.

Calculate the relative power using the formula: Relative Power = (Power / Max Power). Then, plot the Relative Power (%) against time to visualize the data.

We observe some variability in the power output for the 385 nm light source.
To assess the stability:
Define a Stability Duration Window:
Select a time period (e.g., 10 minutes) during which the power output should remain stable.Specify a Maximum Coefficient of Variation (CV) Threshold:
Determine an acceptable variability limit for the selected window (e.g., 0.01%).Calculate the Coefficient of Variation (CV):
Use the formula: CV = (Standard Deviation / Mean)
Compute the CV for the specified stability duration window.Visualize Stability:
Plot the calculated CV over time to analyze the stability of the power output.


We observe that the light sources stabilize quickly, within less than 10 minutes, while the 385 nm light source takes approximately 41 minutes to reach stability.
Report the results in a table
| 385nm | 475nm | 555nm | 630nm | |
| Stabilisation time (Max CV 0.01% for 10 min) | 41 | 3 | 3 | 8 |
| Stability Factor (%) Before Warmup | 99.7% | 99.9% | 100.0% | 100.0% |
| Stability Factor (%) After Warmup | 100.0% | 100.0% | 100.0% | 99.9% |
Selected Stability Duration Window (min): 10 min and Maximum Coefficient of Variation: 0.01%
Conclusion
The illumination warm-up time for this instrument is approximately 40 minutes. This duration is essential for ensuring accurate quantitative measurements, as the Coefficient of Variation (CV) threshold is strict, with a maximum allowable variation of 0.01% within a 10-minute window.
Illumination Maximum Power Output
This measure assesses the maximum power output of each light source, considering both the quality of the light source and the components along the light path. Over time, we expect a gradual decrease in power output due to the aging of hardware, including the light source and other optical components. These measurements will also be used to track the performance of the light sources over their lifetime (see Long-Term Illumination Stability section). For a detailed exploration of illumination properties, refer to the Illumination Power, Stability, and Linearity Protocol by the QuaRep Working Group 01.
Acquisition protocol
- Warm up the light sources for the required duration (see previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Center the sensor with the objective to ensure proper alignment.
- Zero the sensor to ensure accurate readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn the light source on to 100% power.
- Record the average power output over 10 seconds.I personally re-use the data collected during the warm-up kinetic experiment (when the power is stable) for this purpose.
- Repeat steps 5 to 7 for each light source and wavelength you wish to monitor.
Results
Fill in the orange cells in the Illumination_Maximum Power Output_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured maximum power output (in mW).

Plot the measured maximum power output (in mW) and compare it to the manufacturer’s specifications. Calculate the Relative Power using the formula: Relative Power = (Measured Power / Manufacturer Specifications) and plot the relative power for each light source

Report the results in a table
| Manufacturer Specifications (mW) | Measurements 2024-11-22 (mW) | Relative Power (%) | |
| 385nm | 150.25 | 122.2 | 81% |
| 470nm | 110.4 | 95.9 | 87% |
| 555nm | 31.9 | 24 | 75% |
| 630nm | 52 | 39.26 | 76% |
Conclusion
This instrument provides 80% of the power specified by the manufacturer. These results are consistent, as the manufacturer’s specifications are based on a different objective, and likely different filters and mirrors, which can affect the measured power output.
Illumination Stability
The light sources used on a microscope should remain constant or at least stable over the time scale of an experiment. For this reason, illumination stability is recorded across four different time scales:
- Real-time Illumination Stability: Continuous recording for 1 minute. This represents the duration of a z-stack acquisition.
- Short-term Illumination Stability: Recording every 1-10 seconds for 5-15 minutes. This represents the duration needed to acquire several images.
- Mid-term Illumination Stability: Recording every 10-30 seconds for 1-2 hours. This represents the duration of a typical acquisition session or short time-lapse experiments. For longer time-lapse experiments, a longer duration may be used.
- Long-term Illumination Stability: Recording once a year or more over the lifetime of the instrument.
For a detailed exploration of illumination stability, refer to the Illumination Power, Stability, and Linearity Protocol by the QuaRep Working Group 01.
Real-time Illumination Stability
Acquisition protocol
- Warm up the light sources for the required duration (see previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Center the sensor with the objective to ensure proper alignment.
- Zero the sensor to ensure accurate readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn the light source on to 100% power.
- Record the power output every 100 ms for 1 minute. For some microscope dedicated to a fast imaging it might be required to record stability at a faster rate. The THorlab S170C sensor can record at 1 kHz
I personally acquire this data immediately after the warm-up kinetic experiment, without turning off the light source.
- Repeat steps 5 to 7 for each light source and wavelength you wish to monitor.
Results
Fill in the orange cells in the Illumination_Stability_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured power output (in mW) over time.

Calculate the relative power using the formula: Relative Power = (Power / Max Power). Then, plot the Relative Power (%) over time.

Calculate the Stability Factor (S) using the formula: S (%) = 100 × (1 - (Pmax - Pmin) / (Pmax + Pmin)). Also, calculate the Coefficient of Variation (CV) using the formula: CV = Standard Deviation / Mean. Reports the results in a table.
| Stability Factor | Coefficient of Variation | |
| 385nm | 99.99% | 0.002% |
| 475nm | 99.99% | 0.002% |
| 555nm | 99.97% | 0.004% |
| 630nm | 99.99% | 0.002% |
From the Stability Factor results, we observe that the difference between the maximum and minimum power is less than 0.03%. Additionally, the Coefficient of Variation indicates that the standard deviation is less than 0.004% of the mean value, demonstrating excellent power stability.
Conclusion
The light sources exhibit a very high stability, >99.9% during a 1-minute period.
Short-term Illumination Stability
Acquisition protocol
- Warm up the light sources for the required duration (see previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Ensure the sensor is properly centered with the objective for accurate measurements.
- Zero the sensor to ensure precise readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the desired wavelength of the light source.
- Turn on the light source to 100% intensity.
- Record the power output every 10 seconds for 15 minutes.
I personally re-use the data collected during the warm-up kinetic experiment (when the power is stable) for this purpose.
- Repeat steps 5 to 7 for each light source you wish to monitor.
Results
Fill in the orange cells in the Illumination_Stability_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured power output (in mW) over time.

Calculate the relative power using the formula: Relative Power = Power / Max Power. Then, plot the Relative Power (%) over time.

Calculate the Stability Factor (S) using the formula: S (%) = 100 × (1 - (Pmax - Pmin) / (Pmax + Pmin)). Also, calculate the Coefficient of Variation (CV) using the formula: CV = Standard Deviation / Mean. Reports the results in a table.
| Stability Factor | Coefficient of Variation | |
| 385nm | 100.00% | 0.000% |
| 475nm | 100.00% | 0.002% |
| 555nm | 100.00% | 0.003% |
| 630nm | 99.99% | 0.004% |
From the Stability Factor results, we observe that the difference between the maximum and minimum power is less than 0.01%. Additionally, the Coefficient of Variation indicates that the standard deviation is less than 0.004% of the mean value, demonstrating excellent power stability.
Conclusion
The light sources exhibit high stability, maintaining >99.9% stability during a 15-minute period.
Mid-term Illumination Stability
Acquisition protocol
- Warm up the light sources for the required duration (see previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Ensure the sensor is properly centered with the objective for accurate measurements.
- Zero the sensor to ensure precise readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the desired wavelength of the light source.
- Turn on the light source to 100% intensity.
- Record the power output every 10 seconds for 1 hour.
I personally re-use the data collected during the warmup kinetic experiment.
- Repeat steps 5 to 7 for each light source you wish to monitor
Results
Fill in the orange cells in the Illumination_Stability_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured power output (in mW) over time to assess stability.

Calculate the relative power using the formula: Relative Power = Power / Max Power. Then, plot the Relative Power (%) over time.

Calculate the Stability Factor (S) using the formula: S (%) = 100 × (1 - (Pmax - Pmin) / (Pmax + Pmin)). Also, calculate the Coefficient of Variation (CV) using the formula: CV = Standard Deviation / Mean. Reports the results in a table.
| Stability Factor | Coefficient of Variation | |
| 385nm | 99.98% | 0.013% |
| 475nm | 99.98% | 0.011% |
| 555nm | 99.99% | 0.007% |
| 630nm | 99.97% | 0.020% |
From the Stability Factor results, we observe that the difference between the maximum and minimum power is less than 0.03%. Additionally, the Coefficient of Variation indicates that the standard deviation is less than 0.02% of the mean value, demonstrating excellent power stability.
Conclusion
The light sources exhibit exceptional stability, maintaining a performance of >99.9% during a 1-hour period.
Long-term Illumination Stability
Long-term illumination stability measures the power output over the lifetime of the instrument. Over time, we expect a gradual decrease in power output due to the aging of hardware, including the light source and other optical components. These measurements are not an experiment per se but it is the measurement of the maximum power output over time.
Acquisition protocol
- Warm up the light sources for the required duration (see previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Center the sensor with the objective to ensure proper alignment.
- Zero the sensor to ensure accurate readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn the light source on to 100% power.
- Record the average power output over 10 seconds.I personally re-use the data collected for the maximal power output section and plot it over time.
- Repeat steps 5 to 7 for each light source and wavelength you wish to monitor.
Results
Fill in the orange cells in the Illumination_Stability_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured power output (in mW) over time to assess the stability of the illumination.
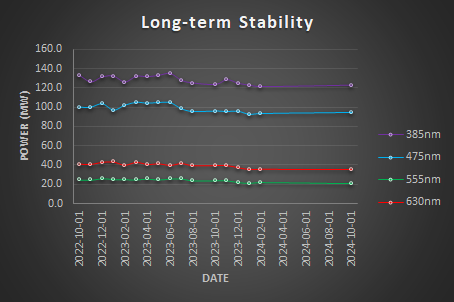
Calculate the relative power using the formula: Relative Power = Power / Max Power. Then, plot the Relative Power (%) over time.

Calculate the Relative PowerSpec by comparing the measured power to the manufacturer’s specifications using the following formula: Relative PowerSpec = Power / PowerSpec. Then, plot the Relative PowerSpec (% Spec) over time.

We expect a gradual decrease in power output over time due to the aging of hardware. Light sources should be replaced when the Relative PowerSpec falls below 50%.
Reports the results in a table.
| Stability Factor | Coefficient of Variation | |
| 385nm | 94.51% | 3.49% |
| 475nm | 93.59% | 4.42% |
| 555nm | 88.96% | 6.86% |
| 630nm | 89.46% | 6.71% |
Conclusion
The light sources are somehow stable over the last 2 years but a decrease in the maximum power output is seen.
Illumination Stability Conclusions
Real-time 1 min | Short-term 15 min | Mid-term 1 h | |
385nm | 99.99% | 100.00% | 99.98% |
475nm | 99.99% | 100.00% | 99.98% |
555nm | 99.97% | 100.00% | 99.99% |
630nm | 99.99% | 99.99% | 99.97% |
The light sources are highly stable (>99.9%).
Illumination Input-Output Linearity
This measure compares the power output as the input varies. A linear relationship is expected between the input and the power output. For a detailed exploration of illumination linearity, refer to the Illumination Power, Stability, and Linearity Protocol by the QuaRep Working Group 01.
Acquisition protocol
- Warm up the light sources for the required duration (refer to the previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Ensure the sensor is properly centered with the objective for accurate measurements.
- Zero the sensor to ensure precise readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn on the light source and adjust its intensity to 0%, then incrementally increase to 10%, 20%, 30%, and so on, up to 100%.I typically collect this data immediately after the warm-up kinetic phase and once the real-time power stability data has been recorded.
- Record the power output corresponding to each input level.
- Repeat steps 5 to 7 for each light source you wish to monitor
Results
Fill in the orange cells in the Illumination_Linearity_Template.xlsx spreadsheet to visualize your results. For each light source, plot the measured power output (in mW) as a function of the input (%).

Calculate the Relative Power using the formula: Relative Power = Power / MaxPower. Then, plot the Relative Power (%) as a function of the input (%).

Determine the equation for each curve, which is typically a linear relationship of the form: Output = K × Input. Report the slope (K) and the coefficient of determination (R²) for each curve in a table.
Illumination Input-Output Linearity | ||
Slope | R2 | |
385nm | 0.9969 | 1 |
475nm | 0.9984 | 1 |
555nm | 1.0012 | 1 |
630nm | 1.0034 | 1 |
The slopes demonstrate a nearly perfect linear relationship between the input and the measured output power, with values very close to 1. The coefficient of determination (R²) indicates a perfect linear fit, showing no deviation from the expected relationship.
Conclusion
The light sources are highly linear.
Objectives and Cubes Transmittance
Since we are using a power meter, we can easily assess the transmittance of the objectives and filter cubes. This measurement compares the power output when different objectives and filter cubes are in the light path. It evaluates the transmittance of each objective and compares it with the manufacturer’s specifications. This method can help detect defects or dirt on the objectives. It can also verify the correct identification of the filters installed in the microscope.
Objectives Transmittance
Acquisition protocol
- Warm up the light sources for the required duration (refer to the previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Ensure the sensor is properly centered with the objective.
- Zero the sensor to ensure accurate readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn on the light source to 100% intensity.
- Record the power output for each objective, as well as without the objective in place.
I typically collect this data after completing the warm-up kinetic phase, followed by the real-time power stability measurements, and immediately after recording the power output linearity.
- Repeat steps 5 to 7 for each light source and wavelength
Results
Fill in the orange cells in the Objective and cube transmittance_Template.xlsx spreadsheet to visualize your results. For each objective, plot the measured power output (in mW) as a function of the wavelength (in nm).

Calculate the Relative Transmittance using the formula: Relative Transmittance = Power / PowerNoObjective. Then, plot the Relative Transmittance (%) as a function of the wavelength (in nm).

Calculate the average transmittance for each objective and report the results in a table. Compare the average transmittance to the specifications provided by the manufacturer to assess performance.
| Average Transmittance | Specifications [470-630] | Average Transmittance | |
| 2.5x-0.075 | 77% | >90% | 84% |
| 10x-0.25-Ph1 | 60% | >80% | 67% |
| 20x-0.5 Ph2 | 62% | >80% | 68% |
| 63x-1.4 | 29% | >80% | 35% |
The measurements are generally close to the specifications, with the exception of the 63x-1.4 objective. This deviation is expected, as the 63x objective has a smaller back aperture, which reduces the amount of light it can receive. Additionally, you can compare the shape of the transmittance curves to further assess performance.
Conclusion
The objectives are transmitting light properly.
Cubes Transmittance
Acquisition protocol
- Warm up the light sources for the required duration (refer to the previous section).
- Place the power meter sensor (e.g., Thorlabs S170C) on the microscope stage.
- Ensure the sensor is properly centered with the objective.
- Zero the sensor to ensure accurate readings.
- Using your power meter controller (e.g., Thorlabs PM400) or software, select the wavelength of the light source you wish to monitor.
- Turn on the light source to 100% intensity.
- Record the power output for each filter cube.
I typically collect this data after completing the warm-up kinetic phase, followed by the real-time power stability measurements, and immediately after recording the power output linearity.
- Repeat steps 5 to 7 for each light source and wavelength
Results
Fill in the orange cells in the Objective and cube transmittance_Template.xlsx spreadsheet to visualize your results. For each filter cube, plot the measured power output (in mW) as a function of the wavelength (in nm).

Calculate the Relative Transmittance using the formula: Relative Transmittance = Power / PowerMaxFilter. Then, plot the Relative Transmittance (%) as a function of the wavelength (in nm).

Calculate the average transmittance for each filter at the appropriate wavelengths and report the results in a table.
| 385 | 475 | 555 | 590 | 630 | |
| DAPI/GFP/Cy3/Cy5 | 100% | 100% | 100% | 100% | 100% |
| DAPI | 14% | 0% | 0% | 8% | 0% |
| GFP | 0% | 47% | 0% | 0% | 0% |
| DsRed | 0% | 0% | 47% | 0% | 0% |
| DHE | 0% | 0% | 0% | 0% | 0% |
| Cy5 | 0% | 0% | 0% | 0% | 84% |
The DAPI cube transmits only 14% of the excitation light compared to the Quad Band Pass DAPI/GFP/Cy3/Cy5. While it is still usable, it will provide a low signal. This is likely because the excitation filter within the cube does not match the light source properly. Since an excitation filter is already included in the light source, the filter in this cube could be removed.
The GFP and DsRed cubes transmit 47% of the excitation light compared to the Quad Band Pass DAPI/GFP/Cy3/Cy5, and they are functioning properly.
The DHE cube does not transmit any light from the Colibri. This cube may need to be removed and stored.
The Cy5 cube transmits 84% of the excitation light compared to the Quad Band Pass DAPI/GFP/Cy3/Cy5, and it is working properly.
Conclusion
Actions to be Taken:
- Remove the excitation filter from the DAPI cube, as it does not properly match the light source and is redundant with the excitation filter already included in the light source.
- Remove and store the DHE cube, as it does not transmit any light from the Colibri and is no longer functional.
We are done with the powermeter .
Field Illumination Uniformity
Having confirmed the stability of our light sources and verified that the optical components (objectives and filter cubes) are transmitting light effectively, we can now proceed to evaluate the uniformity of the illumination. This step assesses how evenly the illumination is distributed. For a comprehensive guide on illumination uniformity, refer to the Illumination Uniformity by the QuaRep Working Group 03.
Acquisition protocol
- Place a fluorescent plastic slide (Thorlabs FSK5) onto the stage.
- Center the slide and the objective.
- Adjust the focus to align with the surface of the slide.
I typically use a red fluorescent slide and focus on a scratch mark on its surface for alignment.
Slightly adjust the focus deeper into the slide to minimize the visibility of dust, dirt, and scratches.
Modify the acquisition parameters to ensure the image is properly exposed.
I typically use the auto-exposure feature, aiming for a targeted intensity of 30%.
- Capture a multi-channel image.
- Repeat steps 5 and 6 for each objective and filter combination.
Results
You should have acquired several multi-channel images that now need processing to yield meaningful results. To process them, use the Field Illumination analysis feature of the MetroloJ_QC plugin for FIJI. For more information about the MetroloJ_QC plugin please refer to manual available at the MontpellierRessourcesImagerie on GitHub.
- Open FIJI.
- Load your image by dragging it into the FIJI bar.
- Launch the MetroloJ_QC plugin by navigating to Plugins > MetroloJ QC.
- Click on Field Illumination Report.
- Enter a title for your report.
- Type in your name.
- Click Filter Parameters and input the filter's names, excitation, and emission wavelengths.
Check Remove Noise using Gaussian Blur.
Enable Apply Tolerance to the Report and reject uniformity and accuracy values below 80%.
Click File Save Options.
Select Save Results as PDF Reports
Select Save Results as spreadsheets.
Click OK.
Repeat steps 4 through 13 for each image you have acquired.
This will generate detailed results stored in a folder named Processed. The Processed folder will be located in the same directory as the original images, with each report and result saved in its own sub-folder.
Use the following R script to merge all _results.xls files into a single file.
This script will load all _results.xls files located in the "Input" folder on your desktop or prompt you to select an input folder.
It will compile and merge data generated by the MetroloJ_QC Field Illumination analysis, including metrics such as Uniformity and Centering Accuracy for each channel from every file.
Additionally, it will split the filenames using the _ character and create columns named Variable-001, Variable-002, etc. This will help in organizing the data if the filenames are formatted as Objective_VariableA_VariableB, for example.
The combined data will be saved as Combined_output.csv in the Output folder on your desktop.
# Clear the workspace
rm(list = ls())
# Set default input and output directories
default_input_dir <- file.path(Sys.getenv("USERPROFILE"), "Desktop", "Input") # Default to "Input" on Desktop
InputFolder <- default_input_dir # Use default folder
# Prompt user to select a folder (optional, currently commented)
InputFolder <- choose.dir(default = default_input_dir, caption = "Select an Input Folder") # You may comment this line if you want to directly use the InputFolder on your desktop
# If no folder is selected, fall back to the default
if (is.na(InputFolder)) {
InputFolder <- default_input_dir
}
# Specify the Output folder (this is a fixed folder on the Desktop)
OutputFolder <- file.path(Sys.getenv("USERPROFILE"), "Desktop", "Output")
if (!dir.exists(OutputFolder)) dir.create(OutputFolder, recursive = TRUE)
# List all XLS files ending with "_results.xls" in the folder and its subfolders
xls_files <- list.files(path = InputFolder, pattern = "_results.xls$", full.names = TRUE, recursive = TRUE)
if (length(xls_files) == 0) stop("No _results.xls files found in the selected directory.")
# Define the header pattern to search for
header_pattern <- "Filters combination/set.*Uniformity.*Field Uniformity.*Centering Accuracy.*Image.*Coef. of Variation.*Mean c fit value"
# Initialize a list to store tables
all_tables <- list()
# Loop over all XLS files
for (file in xls_files) {
# Read the file as raw lines (since it's tab-separated)
lines <- readLines(file)
# Find the line that matches the header pattern
header_line_index <- grep(header_pattern, lines)
if (length(header_line_index) == 0) {
cat("No matching header found in file:", file, "\n")
next # Skip this file if the header isn't found
}
# Extract the table starting from the header row
start_row <- header_line_index[1]
# The table might end at an empty line, so let's find the next empty line after the header
end_row <- min(grep("^\\s*$", lines[start_row:length(lines)]), na.rm = TRUE) + start_row - 1
if (is.na(end_row)) end_row <- length(lines) # If no empty line found, use the last line
# Extract the table rows (lines between start_row and end_row)
table_lines <- lines[start_row:end_row]
# Convert the table lines into a data frame
table_data <- read.table(text = table_lines, sep = "\t", header = TRUE, stringsAsFactors = FALSE)
# Add the filename as the first column (without extension)
filename_no_extension <- tools::file_path_sans_ext(basename(file))
table_data$Filename <- filename_no_extension
# Split the filename by underscores and add as new columns
filename_parts <- unlist(strsplit(filename_no_extension, "_"))
for (i in 1:length(filename_parts)) {
table_data[[paste0("Variable-", sprintf("%03d", i))]] <- filename_parts[i]
}
# Rename columns based on the exact names found in the data
colnames(table_data) <- gsub("Filters.combination.set", "Channel", colnames(table_data))
colnames(table_data) <- gsub("Uniformity....", "Uniformity (%)", colnames(table_data))
colnames(table_data) <- gsub("Field.Uniformity....", "Field Uniformity (%)", colnames(table_data))
colnames(table_data) <- gsub("Centering.Accuracy....", "Centering Accuracy (%)", colnames(table_data))
colnames(table_data) <- gsub("Coef..of.Variation", "CV", colnames(table_data))
# Remove the "Mean.c.fit.value" column if present
colnames(table_data) <- gsub("Mean.c.fit.value", "", colnames(table_data))
# Drop any columns that were renamed to an empty string
table_data <- table_data[, !grepl("^$", colnames(table_data))]
# Divide the relevant columns by 100 to convert percentages into decimal values
table_data$`Uniformity (%)` <- table_data$`Uniformity (%)` / 100
table_data$`Field Uniformity (%)` <- table_data$`Field Uniformity (%)` / 100
table_data$`Centering Accuracy (%)` <- table_data$`Centering Accuracy (%)` / 100
# Store the table in the list with the file name as the name
all_tables[[basename(file)]] <- table_data
}
# Check if any tables were extracted
if (length(all_tables) == 0) {
stop("No tables were extracted from the files.")
}
# Optionally, combine all tables into a single data frame (if the structures are consistent)
combined_data <- do.call(rbind, all_tables)
# View the combined data
#head(combined_data)
# Optionally, save the combined data to a CSV file
output_file <- file.path(OutputFolder, "combined_output.csv")
write.csv(combined_data, output_file, row.names = FALSE)
cat("Combined data saved to:", output_file, "\n")
The following spreadsheet provides a dataset that can be manipulated with a pivot table to generate informative graphs and statistics Illumination_Uniformity_Template.xlsx. Plot the uniformity and centering accuracy for each objective.

| Objective | Uniformity | Centering Accuracy |
| 2x | 97.5% | 92.7% |
| 10x | 97.0% | 94.5% |
| 20x | 97.3% | 97.1% |
| 63x | 96.6% | 96.7% |
Plot the uniformity and centering accuracy for each filter set.

| Filter | Uniformity | Centering Accuracy |
| DAPI | 98.3% | 99.4% |
| DAPIc | 95.8% | 84.9% |
| GFP | 98.1% | 99.1% |
| GFPc | 96.5% | 93.3% |
| Cy3 | 97.6% | 96.5% |
| Cy3c | 96.8% | 97.9% |
| Cy5 | 97.0% | 99.6% |
| Cy5c | 96.7% | 91.3% |
This specific instrument has a quad-band filter as well as individual filter cubes. We can plot the uniformity and centering accuracy per filter types.

| Filter Type | Uniformity | Centering Accuracy |
Quad band | 97.7% | 98.7% |
| Single band | 96.5% | 91.8% |
Conclusion
The uniformity and centering accuracy are excellent across all objectives and filters, consistently exceeding 90%. However, the single-band filter cubes exhibit slightly lower uniformity and centering accuracy compared to the quad-band filter cube.
XYZ Drift
This experiment evaluates the stability of the system in the XY and Z directions. As noted earlier, when an instrument is started, it requires a warmup period to reach a stable steady state. To determine the duration of this phase accurately, it is recommended to record a warmup kinetic at least once per year.
Acquisition protocol
Place 4 µm diameter fluorescent beads (TetraSpec Fluorescent Microspheres Size Kit, mounted on a slide) on the microscope stage.
Center an isolated bead under a high-NA dry objective.
- Crop the acquisition area to only visualize one bead but keep it large enough to anticipate a potential drift along the X and Y axes (100 um FOV should be enough)
Select an imaging channel appropriate for the fluorescent beads
I typically use the Cy5 channel which is very bright and resistant to bleaching, yet this channel has a lower resolution, but it does not really matter here
Acquire a large Z-stack at 1-minute intervals for a duration of 24 hours.
To ensure accurate measurements, it is essential to account for potential drift along the Z-axis by acquiring a Z-stack that is substantially larger than the visible bead size. I typically acquire a 40 µm Z-stack.
Results
- Open your image in FIJI
- If necessary, crop the image to focus on a single bead for better visualization.
- Use the TrackMate plugin included in FIJI to detect and track spots over time Plugins\Tracking\TrackMate.
- Apply Difference of Gaussians (DoG) spot detection with a detection size of 4 µm
- Enable sub-pixel localization for increased accuracy
- Click Preview to visualize the spot detection
- Set a quality threshold (click and slide) high enough to detect a single spot per frame
- Click Next and follow the detection and tracking process
- Save the detected Spots coordinates as a CSV file for further analysis
Open the spreadsheet template XYZ Drift Kinetic_Template.xlsx and fill in the orange cells. Copy and paste the XYZT and Frame columns from the TrackMate spots CSV file into the corresponding orange columns in the spreadsheet. Enter the numerical aperture (NA) and emission wavelength used during the experiment. Calculate the relative displacement in X, Y, and Z using the formula: Relative Displacement = Position - PositionInitial. Finally, plot the relative displacement over time to visualize the system's drift.


Identify visually the time when the displacement is lower than the resolution of the system. On this instrument it takes 120 min to reach its stability. Calculate the velocity, Velocity = (Displacement2-Displacement1)/T2-T1) and plot the velocity over time.

Calculate the average velocity before and after stabilisation and report the results in a table.
| Objective NA | 0.5 |
| Wavelength (nm) | 705 |
| Resolution (nm) | 705 |
| Stabilisation time (min) | 122 |
| Average velocity Warmup (nm/min) | 113 |
| Average velocity System Ready (nm/min) | 14 |
Conclusion
The warmup time for this instrument is approximately 2 hours. After the warmup period, the average displacement velocity is 14 nm/min, which falls within an acceptable range.
XYZ Repositioning accuracy
This experiment evaluates how accurate is the system in XY by measuring the accuracy of repositioning. Several variables can affect repositioning accuracy: i) Time, ii) Traveled distance, iii) Speed and iv) acceleration. For a detailed exploration of Stage repositioning accuracy refer to the XY Repositioning Protocol by the QuaRep Working Group 06.
Acquisition protocol
Place 4 µm diameter fluorescent beads (TetraSpec Fluorescent Microspheres Size Kit, mounted on a slide) on the microscope stage.
Center an isolated bead under a high-NA dry objective.
- Crop the acquisition area to only visualize one bead but keep it large enough to anticipate a potential drift along the X and Y axes (100 um FOV should be enough)
Select an imaging channel appropriate for the fluorescent beads
I typically use the Cy5 channel which is very bright and resistant to bleaching, yet this channel has a lower resolution.
Acquire a Z-stack at positions separated by 0 um (Drift), 1000 um and 10 000 um in both X and Y direction.
Repeat the acquisition 20 times
Acquire 3 datasets for each condition
- Your stage might have a smaller range!
- Lower the objectives during movement to avoid damage
Results
- Open your image in FIJI
- If necessary, crop the image to focus on a single bead for better visualization.
- Use the TrackMate plugin included in FIJI to detect and track spots over time Plugins\Tracking\TrackMate.
- Apply Difference of Gaussians (DoG) spot detection with a detection size of 4 µm
- Enable sub-pixel localization for increased accuracy
- Click Preview to visualize the spot detection
- Set a quality threshold (click and slide) high enough to detect a single spot per frame
- Click Next and follow the detection and tracking process
- Save the detected Spots coordinates as a CSV file for further analysis
Open the spreadsheet template XY Repositioning Accuracy_Template.xlsx and fill in the orange cells. Copy and paste the XYZT and Frame columns from the TrackMate spots CSV file into the corresponding orange columns in the spreadsheet. Enter the numerical aperture (NA) and emission wavelength used during the experiment. Calculate the relative positionin X, Y, and Z using the formula: Relative PositionRelative = Position - PositionInitial. Finally, plot the relative position over time to visualize the system's stage repositioning accuracy.



We observe an initial movement in X and Y that stabilises. Calculate the displacement 2D Displacement = Sqrt( (X2-X1)2 + (Y2-Y1)2) ) and plot the 2D displacement over time. Calculate the resolution of your imaging configuration, Lateral Resolution = LambdaEmission / 2*NA and plot the resolution over time (constant).



This experiment shows an initial hight displacement between 1000 and 400nm (Frame 1) that reduces to 70nm at Frame 2. Calculate the Accuracy for each parameter using the formula Accuracy = Standard Deviation (Value) and report them in a table.
| Traveled Distance (um) | 0 | 1000 | 10000 |
| X Accuracy (nm) | 4 | 188 | 121 |
| Y Accuracy (nm) | 4 | 141 | 48 |
| Z Accuracy (nm) | 10 | 34 | 53 |
| Repositioning Accuracy 3D (nm) | 6 | 227 | 91 |
| Repositioning Accuracy 2D (nm) | 2 | 226 | 90 |
Conclusion
The system has a stage accuracy of 230 nm. The results are both interesting and unexpected, as there is an initial shift in the first frame that eventually stabilizes. Excluding the first frame significantly improves the measurements, reducing the accuracy to 40 nm. Further investigation is required to understand the underlying cause.
| Traveled Distance (um) | 0 | 1000 | 10000 |
| X Accuracy (nm) | 3 | 28 | 52 |
| Y Accuracy (nm) | 3 | 68 | 35 |
| Z Accuracy (nm) | 10 | 26 | 40 |
| Repositioning Accuracy 3D (nm) | 6 | 43 | 36 |
| Repositioning Accuracy 2D (nm) | 2 | 40 | 36 |
Deeper Investigation
We observed a significant shift in the first frame, which was unexpected and invites further investigation. These variables can affect repositioning accuracy: i) Traveled distance, ii) Speed, iii) Acceleration, iv) Time, and v) Environment. We decided to test the first three. To do this, we followed the XYZ repositioning accuracy protocol with the following parameters:
- Distances: 0um, 1um, 10um, 1000um, 10 000um, 30 000um
- Speed: 10%, 100%
- Acceleration: 10%,100%
- For each conditions 3 datasets were acquired
This experimental protocol generated a substantial number of images. To process them automatically in ImageJ/FIJI using the TrackMate plugin, we use the following script Batch Track Opened Images with TrackMate.py
# --------------------------
# User Prompt Toggle
# --------------------------
# Set this to False to skip the initial dialog and reuse previous settings
show_initial_prompt = True # Change this as needed
import os
import sys
import json
from ij import IJ, WindowManager
from java.io import File
from ij.gui import GenericDialog
from fiji.plugin.trackmate import Model, Settings, TrackMate, SelectionModel, Logger
from fiji.plugin.trackmate.detection import DogDetectorFactory
from fiji.plugin.trackmate.tracking.jaqaman import SparseLAPTrackerFactory
from fiji.plugin.trackmate.features import FeatureFilter
from fiji.plugin.trackmate.features.track import TrackIndexAnalyzer
from fiji.plugin.trackmate.gui.displaysettings import DisplaySettingsIO
from fiji.plugin.trackmate.gui.displaysettings.DisplaySettings import TrackMateObject
from fiji.plugin.trackmate.visualization.table import TrackTableView
from fiji.plugin.trackmate.visualization.hyperstack import HyperStackDisplayer
# Ensure UTF-8 encoding
reload(sys)
sys.setdefaultencoding('utf-8')
# Path to the config file that will store last user settings
config_file_path = os.path.join(os.path.expanduser("~"), "Desktop", "trackmate_config.json")
# Default settings in case there's no previous config file
default_settings = {
'subpixel_localization': True,
'spot_diameter': 4.0, # Default 0.5 microns
'threshold_value': 20.904, # Default threshold value
'apply_median_filtering': False
}
# Function to load settings from the config file
def load_settings():
if os.path.exists(config_file_path):
with open(config_file_path, 'r') as f:
return json.load(f)
else:
return default_settings
# Function to save settings to the config file
def save_settings(settings):
with open(config_file_path, 'w') as f:
json.dump(settings, f)
# Load previous settings (or use default if no file exists)
user_settings = load_settings()
# Create output directory on the user's desktop
output_dir = os.path.join(os.path.expanduser("~"), "Desktop", "Output")
if not os.path.exists(output_dir):
os.makedirs(output_dir)
# ----------------------------
# Create the model object
# ----------------------------
model = Model()
model.setLogger(Logger.IJ_LOGGER) # Send messages to the ImageJ log window
# ------------------------
# Create input dialog
# ------------------------
# Create the dialog box for user input
gd = GenericDialog("TrackMate Parameters")
# Add fields to the dialog, prefill with last saved values
gd.addCheckbox("Enable Subpixel Localization?", user_settings['subpixel_localization']) # Default: from saved settings
gd.addNumericField("Spot Diameter (microns):", user_settings['spot_diameter'], 2) # Default diameter: from saved settings
gd.addSlider("Threshold Value:", 0, 255, user_settings['threshold_value']) # Slider for threshold value (0-255 range, default: from saved settings)
gd.addCheckbox("Apply Median Filtering?", user_settings['apply_median_filtering']) # Default: from saved settings
gd.addCheckbox("Process All Open Images?", False) # Add a checkbox to select processing mode
# Show the dialog
gd.showDialog()
# Check if the user canceled the dialog
if gd.wasCanceled():
sys.exit("User canceled the operation.")
# Get user inputs from the dialog
subpixel_localization = gd.getNextBoolean() # Whether to enable subpixel localization
spot_diameter = gd.getNextNumber() # Spot diameter in microns
threshold_value = gd.getNextNumber() # Threshold value from the slider
apply_median_filtering = gd.getNextBoolean() # Whether to apply median filtering
process_all_images = gd.getNextBoolean() # Whether to process all open images
# Save the new settings to the configuration file
user_settings = {
'subpixel_localization': subpixel_localization,
'spot_diameter': spot_diameter,
'threshold_value': threshold_value,
'apply_median_filtering': apply_median_filtering
}
save_settings(user_settings)
# ------------------------
# Prepare settings object
# ------------------------
# If processing all images
if process_all_images:
open_images = WindowManager.getImageTitles()
total_images = len(open_images)
if total_images == 0:
IJ.log("No images are open!")
sys.exit("No images are open!")
for idx, title in enumerate(open_images):
imp = WindowManager.getImage(title)
# Ensure the image is not null
if imp is None:
continue
# Get the image title for naming output files
filename = imp.getTitle()
# Configure TrackMate for this image
settings = Settings(imp)
settings.detectorFactory = DogDetectorFactory()
settings.detectorSettings = {
'DO_SUBPIXEL_LOCALIZATION': subpixel_localization, # Set subpixel localization
'RADIUS': spot_diameter / 2, # Convert diameter to radius for detector
'TARGET_CHANNEL': 1, # Target channel (customize if needed)
'THRESHOLD': threshold_value, # User-defined threshold value
'DO_MEDIAN_FILTERING': apply_median_filtering, # Apply median filtering if selected
}
# Configure tracker
settings.trackerFactory = SparseLAPTrackerFactory()
settings.trackerSettings = settings.trackerFactory.getDefaultSettings()
settings.trackerSettings['ALLOW_TRACK_SPLITTING'] = True
settings.trackerSettings['ALLOW_TRACK_MERGING'] = True
# Add all known feature analyzers to compute track statistics
settings.addAllAnalyzers()
# Configure track filters
track_filter = FeatureFilter('TRACK_DISPLACEMENT', 10, False) # Filter tracks with displacement >10 pixels
settings.addTrackFilter(track_filter)
# -------------------
# Instantiate plugin
# -------------------
trackmate = TrackMate(model, settings)
# --------
# Process
# --------
if not trackmate.checkInput():
IJ.log("Error checking input: " + trackmate.getErrorMessage())
continue
if not trackmate.process():
IJ.log("Error during processing: " + trackmate.getErrorMessage())
continue
# ----------------
# Display results
# ----------------
selection_model = SelectionModel(model)
# Read the default display settings
ds = DisplaySettingsIO.readUserDefault()
ds.setTrackColorBy(TrackMateObject.TRACKS, TrackIndexAnalyzer.TRACK_INDEX)
ds.setSpotColorBy(TrackMateObject.TRACKS, TrackIndexAnalyzer.TRACK_INDEX)
# Display tracks and spots on the image
displayer = HyperStackDisplayer(model, selection_model, imp, ds)
displayer.render()
displayer.refresh()
# -----------------
# Export results
# -----------------
# Export spot table as CSV
spot_table = TrackTableView.createSpotTable(model, ds)
output_csv_path = os.path.join(output_dir, filename + "_spots.csv")
spot_table.exportToCsv(File(output_csv_path))
# Close the image after processing
imp.close()
# Update progress bar
IJ.showProgress(idx + 1, total_images)
else:
# If processing only the active image, leave it open after processing
imp = WindowManager.getCurrentImage()
if imp is None:
sys.exit("No image is currently open.")
filename = imp.getTitle()
# Configure TrackMate for this image
settings = Settings(imp)
settings.detectorFactory = DogDetectorFactory()
settings.detectorSettings = {
'DO_SUBPIXEL_LOCALIZATION': subpixel_localization, # Set subpixel localization
'RADIUS': spot_diameter / 2, # Convert diameter to radius for detector
'TARGET_CHANNEL': 1, # Target channel (customize if needed)
'THRESHOLD': threshold_value, # User-defined threshold value
'DO_MEDIAN_FILTERING': apply_median_filtering, # Apply median filtering if selected
}
# Configure tracker
settings.trackerFactory = SparseLAPTrackerFactory()
settings.trackerSettings = settings.trackerFactory.getDefaultSettings()
settings.trackerSettings['ALLOW_TRACK_SPLITTING'] = True
settings.trackerSettings['ALLOW_TRACK_MERGING'] = True
# Add all known feature analyzers to compute track statistics
settings.addAllAnalyzers()
# Configure track filters
track_filter = FeatureFilter('TRACK_DISPLACEMENT', 10, False) # Filter tracks with displacement >10 pixels
settings.addTrackFilter(track_filter)
# -------------------
# Instantiate plugin
# -------------------
trackmate = TrackMate(model, settings)
# --------
# Process
# --------
if not trackmate.checkInput():
IJ.log("Error checking input: " + trackmate.getErrorMessage())
if not trackmate.process():
IJ.log("Error during processing: " + trackmate.getErrorMessage())
# ----------------
# Display results
# ----------------
selection_model = SelectionModel(model)
# Read the default display settings
ds = DisplaySettingsIO.readUserDefault()
ds.setTrackColorBy(TrackMateObject.TRACKS, TrackIndexAnalyzer.TRACK_INDEX)
ds.setSpotColorBy(TrackMateObject.TRACKS, TrackIndexAnalyzer.TRACK_INDEX)
# Display tracks and spots on the image
displayer = HyperStackDisplayer(model, selection_model, imp, ds)
displayer.render()
displayer.refresh()
# -----------------
# Export results
# -----------------
# Export spot table as CSV
spot_table = TrackTableView.createSpotTable(model, ds)
output_csv_path = os.path.join(output_dir, filename + "_spots.csv")
spot_table.exportToCsv(File(output_csv_path))
# Show completion message
IJ.log("Processing Complete!")
This code automates the process of tracking and analyzing spots in images using the TrackMate plugin in ImageJ/FIJI. In brief :
Prompts the user to configure settings, such as enabling subpixel localization, adjusting spot diameter, setting the threshold, and applying median filtering. These settings are either loaded from a previous configuration file or set to defaults.
Allows the user to choose whether to process all open images or just the active one. For each image, it configures the TrackMate detector (using the Difference of Gaussians method) and tracker (SparseLAPTracker), and sets up feature analysis and filtering based on the user's preferences.
Processes the images, tracks spots, and analyzes features using TrackMate.
Displays the results on the images, showing the tracked spots with the chosen colors.
Exports the spot data as a CSV file to a predefined output directory on the desktop.
Saves the user-defined settings to a JSON configuration file for future use.
This code generates a CSV file for each image, resulting in a large number of files that need to be aggregated for further analysis. The following R script XYZ_Repositioning_Accuracy_Script.R can process all CSV files located in a selected folder on your desktop.
# Load and install necessary libraries at the beginning
rm(list = ls())
# Check and install required packages if they are not already installed
if (!require(dplyr)) install.packages("dplyr", dependencies = TRUE)
if (!require(stringr)) install.packages("stringr", dependencies = TRUE)
if (!require(ggplot2)) install.packages("ggplot2", dependencies = TRUE)
if (!require(tcltk)) install.packages("tcltk", dependencies = TRUE)
# Load libraries
library(dplyr)
library(stringr)
library(ggplot2)
library(tcltk)
# Set default input and output directories
default_input_dir <- file.path(Sys.getenv("USERPROFILE"), "Desktop") # Default to "Output" on Desktop
InputFolder <- tclvalue(tkchooseDirectory(initialdir = default_input_dir, title = "Select a folder containing CSV files"))
#InputFolder <- default_input_dir # Use default folder
# Specify the Output folder (this is a fixed folder on the Desktop)
OutputFolder <- file.path(Sys.getenv("USERPROFILE"), "Desktop", "Output")
if (!dir.exists(OutputFolder)) dir.create(OutputFolder, recursive = TRUE)
# List all CSV files in the folder
csv_files <- list.files(path = InputFolder, pattern = "\\.csv$", full.names = TRUE)
if (length(csv_files) == 0) stop("No CSV files found in the selected directory.")
header <- names(read.csv(csv_files[1], nrows = 1))
# Function to clean the filename
clean_filename <- function(filename) {
filename_parts <- strsplit(filename, " - ")[[1]]
cleaned_filename <- sub("\\.czi", "", filename_parts[1])
cleaned_filename <- sub("_spots", "", cleaned_filename)
cleaned_filename <- sub("\\.csv", "", cleaned_filename)
return(cleaned_filename)
}
# Read and merge all CSV files
merged_data <- csv_files %>%
lapply(function(file) {
data <- read.csv(file, skip = 4, header = FALSE)
colnames(data) <- header
data <- data %>% arrange(FRAME)
# Clean and add source file info
filename <- basename(file)
data$SourceFile <- clean_filename(filename)
# Extract variables from the filename
filename_parts <- strsplit(clean_filename(filename), "_")[[1]]
for (i in seq_along(filename_parts)) {
variable_name <- paste("Variable-", sprintf("%03d", i), sep = "")
data[[variable_name]] <- filename_parts[i]
}
# Add time columns if available
if ("POSITION_T" %in% colnames(data)) {
data$`Time (sec)` <- round(data$POSITION_T, 0)
data$`Time (min)` <- round(data$`Time (sec)` / 60, 2)
}
# Calculate displacement columns (X, Y, Z, 3D, 2D)
if ("POSITION_X" %in% colnames(data)) {
first_value <- data$POSITION_X[data$FRAME == 0][[1]]
data$`X (nm)` <- (data$POSITION_X - first_value) * 1000
}
if ("POSITION_Y" %in% colnames(data)) {
first_value <- data$POSITION_Y[data$FRAME == 0][[1]]
data$`Y (nm)` <- (data$POSITION_Y - first_value) * 1000
}
if ("POSITION_Z" %in% colnames(data)) {
first_value <- data$POSITION_Z[data$FRAME == 0][[1]]
data$`Z (nm)` <- (data$POSITION_Z - first_value) * 1000
}
# Calculate displacement (3D and 2D)
if (all(c("X (nm)", "Y (nm)", "Z (nm)") %in% colnames(data))) {
data$`Displacement 3D (nm)` <- sqrt(
diff(c(0, data$`X (nm)`))^2 +
diff(c(0, data$`Y (nm)`))^2 +
diff(c(0, data$`Z (nm)`))^2
)
data$`Displacement 3D (nm)`[1] <- 0
}
if (all(c("X (nm)", "Y (nm)") %in% colnames(data))) {
data$`Displacement 2D (nm)` <- sqrt(
diff(c(0, data$`X (nm)`))^2 +
diff(c(0, data$`Y (nm)`))^2
)
data$`Displacement 2D (nm)`[1] <- 0
}
return(data)
}) %>%
bind_rows()
# Save the merged data to a new CSV file
output_file <- "XYZ_Repositioning-Accuracy_Data.csv"
write.csv(merged_data, file = file.path(OutputFolder, output_file), row.names = FALSE)
cat("All CSV files have been merged and saved to", output_file, "\n")
This R code automates the processing of multiple CSV files containing spot tracking data. Specifically, it:
- Installs and loads required libraries
- Sets directories for input (CSV files) and output (merged data) on the user's desktop.
- Lists all CSV files in the input directory and reads in the header from the first CSV file.
- Defines a filename cleaning function to extract relevant metadata from the filenames (e.g., removing extensions, and extracting variables).
- Reads and processes each CSV file:
- Skips initial rows and assigns column names.
- Cleans up filenames and adds them to the dataset.
- Calculates displacement in the X, Y, and Z axes relative to the initial position with the formulat PositionRelative= Position - PositionInitial, and computes both 3D and 2D displacement values with the following formulas: 2D_Displacement = Sqrt( (X2-X1)2 + (Y2-Y1)2)); 3D_Displacement = Sqrt( (X2-X1)2 + (Y2-Y1)2) + (Z2-Z1)2 )
- Merges all the processed data into a single dataframe.
- Saves the results as XYZ_Repositioning-Accuracy_Data.csv loated in the Output folder on your desktop that can be further processed and summarized with a pivot table as shown in the following spreadsheet XYZ_Repositioning-Accuracy_Template.xlsx
Using the first frame as a reference we can plot the average XYZ position for each frame.

As seen earlier there is a large displacement between Frame 0 and Frame 1. This is espeically valid for the X axis. We will ignore frame 0 for now and will focus on the varialbes we are interested in is Traveled distance, ii) Speed, iii) Acceleration.
Repositioning Accuracy vs Traveled Distance
Plot the 2D displacement against the frame for each traveled distance.

Data looks good. Now we can calculate the average and the standard deviation of the 2D Displacement and plot it again the traveled distance.



We observe a power relationship which equation is Repositioning Accuracy = 12.76 x Traveled Distance^0.2573
| Traveled Distance (um) | Repositioning Accuracy (nm) |
| 0 | 5 |
| 1 | 12 |
| 10 | 27 |
| 100 | 31 |
| 1000 | 107 |
| 10000 | 121 |
| 30000 | 175 |

In conclusion we observe that the traveled distance significantly affects the repositioning accuracy. However, this accuracy is much lower than the lateral resolution of the system (705nm)
Repositioning accuracy vs Speed and Acceleration

Legend (Wait for it)...
Acquisition protocol
Results
Conclusion
Legend (Wait for it...) dary
Acquisition protocol
Results
Conclusion
References
The information provided here is inspired by the following references:
- No labels